WelcomePhysicsProgrammingPhotographyMeFractalsMisc

Huffman coding in Python using bitarray

(Ilan Schnell, April 2019)

In this article, we explain what Huffman coding is and how Huffman codes can be constructed using Python. Once we construct a Huffman code, we show how the Python bitarray library can be used to efficiently encode and decode data.

Introduction

Almost all computer systems store characters as bytes. For the sake of simplicity, we are only addressing plain English text files that are ASCII encoded. This means that each character is stored as 8 bits. For example the sentence To be or not to be. is represented as 19 bytes, which equals 152 bits. The first letter of the sentence, T is represented by the following eight bits: 01010100. Representing english text in this way appears to be wastful, since only a few number of the 256 different bytes are being used. Our sentence only uses 9 different characters. Obviously a long text will use many more characters, but still much less than 256. Moreover, if we could find a code which represents characters that appear more frequently with shorter bit sequences we could store the sentence in much fewer bits.

Think about Morse code for a second. In Morse code, the letter e is coded as a single dot, whereas letters that are used less often in English text are coded into much longer sequences. For example, the letter 'q' is coded as "dash dot dash dash".

Back to bit sequences. In 1952, American computer scientist David Huffman developed a method for constructing the optimal binary code for a particular message. That is, he developed a system to minimize the binary representation of a particular message. Applying Huffman's method to our sentence To be or not to be., we obtain the following code: 

char   freq    code
---------------------
' '    5       01
'o'    4       000
't'    2       101
'e'    2       111
'b'    2       001
'r'    1       1000
'n'    1       1001
'T'    1       1100
'.'    1       1101

The character that appears most often in this sentence is not a letter but the space symbol. Therefore, the space symbol has a short code: 01. Once we have our (any) code, it is straighforward to encode the message with which we're working. We simply look up the binary code for each character (symbol) in the sentence and then write down those codes (without spaces between them) in the same sequence as the characters in the message. Thus, our sentence To be or not to be. encodes to: 

11000000100111101000100001100100010101101000010011111101

Using Huffman coding, the sentence is only 56 bits long -- as opposed to the original 152 bits. Only about one third!

Decoding these bits is not so easy, because we don't know where each character begins or ends. We need to examine each bit at a time, cross-checking it against our code table until we find a match. Once we find a match, we move on to the next character. The best way to examine bits is using a binary tree, called a Huffman tree, which looks like this:

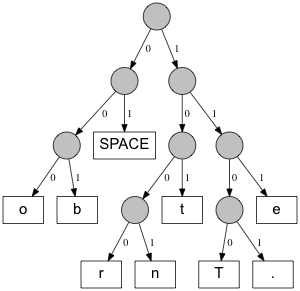
Decoding works by starting at the top of the tree and moving to the left when we encounter a 0 and to the right when we encounter a 1. Once we reach a leaf node we write down the character represented by that leaf node. We repeat this process until the bitsequence we which to decoding ends.

If we look at the decoding process this way, it is obvious, that no code can start with the same bits as another code, because once a leaf node is reached we have to start at the top again.

Constructing the Code

Each node of a Huffman tree is either an internal node, which connects two child nodes, or a leaf node, which represents a particular character. Constructing a Huffman tree allows us to easily figure out the code table, by traversing the tree while keeping track of the branches.

Now, the big question: How did we construct the Huffman code above?

The simplest algorithm for creating a Huffman tree uses a priority queue. A priority queue is a heap of elements in which each element has a priority assigned to it. An element with high priority is removed from the queue before any element with lower priority.

Using such a priority queue, in which nodes with the lowest frequency have the highest priority, the algorithm is:

Because we always remove two nodes from the queue at a time and then add only one new node back to the queue, the number of nodes in the queue is reduced by one with each step of the algorithm until we end up with a single node in the queue.

Python contains an implementation of a priority queue in the heapq module that is part of the standart library. To implement the algorithm described above in Python, we need only the heappush and heappop functions. The heappop function returns the smallest item in the queue, and the heappush function allows us to add new items to the queue. The implementation can be found in the source code of the bitarray project, in the file examples/huffman/huffman.py.

It should be noted that, for a given set of symbols and their frequencies, the algorithm might give us different trees. This will depend on exactly which smallest nodes are popped from the queue in the case where more than two nodes contain the same frequency. However, any resulting Huffman tree will be optimal, meaning that the decoding of the original message will allways result in shortest possible bitsequence. This was mathematically proven by Huffman in 1952.

For our example message, the tree (including frequencies) looks like this:

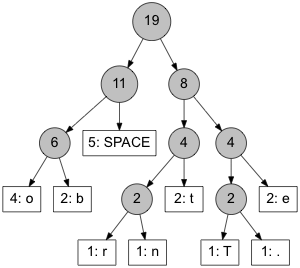
Let us reflect again on the algorithm. Because we always construct new nodes from the two nodes with the lowest frequencies, it is obvious that these low-frequency nodes will end up at the bottom on the tree. This means the path to the lowest frequency nodes will be longest. This is exactly what we want! The symbols that occur the least often should have the longest bit code.

On the other hand, if a node has a very high frequency, it will be added to the tree near the end of the process and, consequently, will be located near the top of the tree. This means the path to the high frequency nodes will be short, resulting into a short bit code.

The above algorithm has a time complexity O(n log n), where n is the number of symbols. There are more efficient algorithms, but as n is a small number compared to the number of symbols in the message to be encoded, we do not worry about the efficiency of creating the Huffman tree. For large messages, the initial frequency count will take far longer than the tree creation itself, and the actual encoding and decoding of messages needs to be efficient.

Encoding and decoding

Now that we are able to construct Huffman codes, we can also encode and decode messages. As discussed earlier, encoding is quite easy: just go through each symbol of the message, look up the code in the code table, and append it to the bitsequence.

Decoding is much harder, because we do not initially know how many bits belong to the symbol we are decoding. Efficient decoding can be achieved by following the nodes in the Huffman tree until reaching a leaf node (and then starting at the top of the tree again until the bitsequence is exhausted).

Until now, we have not discussed the Python bitarray library. When dealing with small data sets, for experimental purposes, it is perfectly fine to represent bitarrays as string sequences of 0 and 1. However, when dealing which much larger data, and when speed becomes an issue, the bitarray library becomes important. Bitarray is written as a Python C extension, and 8 bits are internally stored within one byte of memory. Moreover, all bitarray operations are implemented in C and therefore execute very fast.

Two methods bitarrays expose are .encode() and .decode(). In particular .decode() is extremely efficient, when comparing its performance to a pure Python implementation. The program examples/huffman/decoding.py allows you to compare the speed of bitarray's .decode() method to a pure Python implementation of the same functionality. We have found that for Python 3.7, the Python implementation is about 40 times slower than bitarray's .decode() method, and for Python 2.7 about 80 times slower.

Both these bitarray methods take a code dictionary, i.e. a dict mapping symbols to prefix codes, as an argument. The .decode() method then constructs a tree on the C-level. Constructing a tree from a given code dictionary is very fast and much easier than trying to pass Python tree structure down to the C-level. The C code for this structure is:

/* Binary tree definition */
typedef struct _bin_node
{
    struct _bin_node *child[2];
    PyObject *symbol;
} binode;

Note that child is an array with two elements, each of which are pointers to struct _bin_node itself. Also note that once we have constructed the tree, all leaf nodes will contain only pointers to Python objects, and all internal nodes will contain only pointers to children.

It should not be surprising that traversing a tree with such a simple node structure on the C-level is one to two orders of magnitude faster than traversing Python object nodes on the Python level.

The complete bitarray C implementation is found at bitarray/_bitarray.c.

Real World Example

Finally, let's say we want to compress the size of the ASCII file for the book Pride and Prejudice, by Jane Austen. After counting the frequencies of all symbols, we get the Huffman tree below.

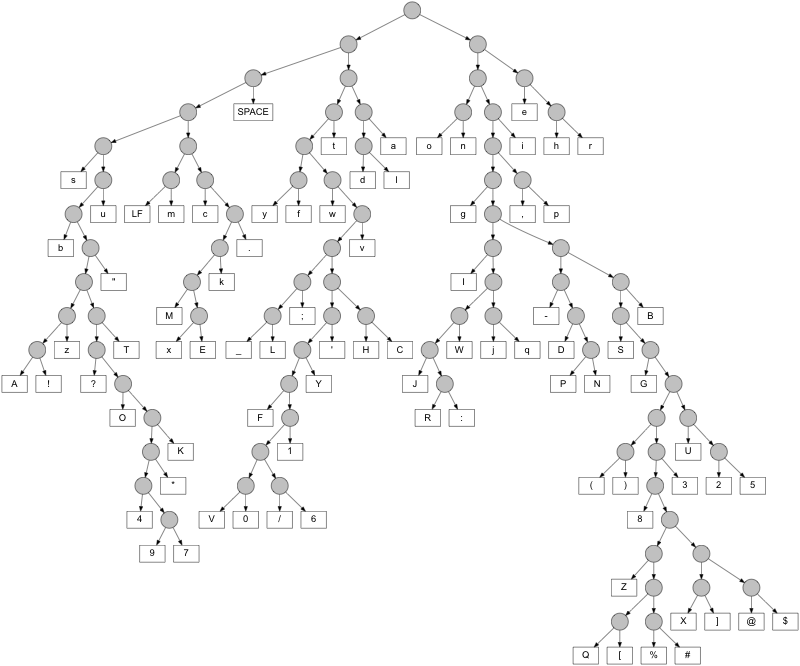
The original text has a file size of 704,175 bytes, which equals 5,633,400 bits. The Huffman encoded bitsequence has a file size of just 3,173,518 bits. So the compression ratio is about 56.3%.

We should note that all the Python code used to create this article, including the .dot files used by graphviz to generate the trees, is available in bitarray Huffman example directory. Also (as of version 1.2.0) the Python bitarray library includes a function to calculate Huffman codes: bitarray.util.huffman_code()