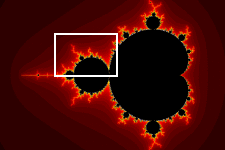
Some of the pictures on my web page show the so-called Mandelbrot Set. The Mandelbrot Set is obtained by the well-known equation

for complex numbers c. All the pictures show a specific region in the complex plane c. Each point in a picture corresponds to a complex number c, and for each of these numbers c, the above equations in iterated until an exit criterion is reached. The number of iterations n required to reach this criterion determines the color of the point in the plane. 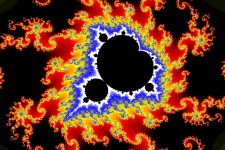This requires a color map which is mapping each n to a certain color. Some pictures only differ in their color map, this means, they show exactly the same region in the complex plane c, but the coloring is different. The color map is very carefully chosen for each picture. The two processes of choosing a region in the complex plane and choosing a color map is what makes creating images of the Mandelbrot Set an art.
Of course, the fascinating feature of the Mandelbrot Set is its fractal nature. This nature can be seen from the pictures at the top and at the bottom of this page. As you can see, the Mandelbrot Set allows you to zoom into any region as often as you wish without loosing the details of the structure. Not only that the structure is not lost, but by zooming into regions, we discover structures that are different from the ones we started from.